Wind Turbine Efficiency

This table is set up to accompany a blog posting about wind turbine efficiency because the tabular data would not display  properly in the blog entry.  The table shown below consists of a range of common wind speeds in mph, since that's the easiest number for Americans to grasp, followed by their equivalent speeds in m/s.  The third column represents the amount of energy present in the wind that moves through an 80 meter diameter wind turbine rotor (5027 m²) at various speeds.  The 4th column represents the Betz Limit which is simply 59% of column three.   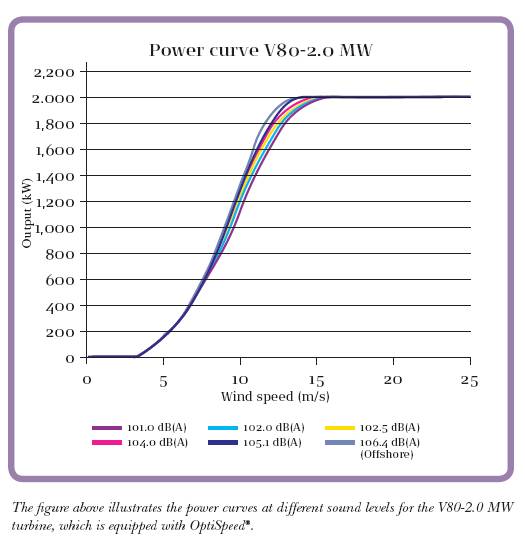The 5th column is derived from the power curve of a Vestas V80 taken from the bottom graph.  The curves are comprised of a range of operating regimes of the V80 turbine based on whether one is trying to optimize efficiency or noise.  I attempted to use the most efficient of these curves to compute numerical values where possible.  The last column is the conversion efficiency vs. the Betz limit when converting the wind energy into electricity.
 

Table of Theoretical, Betz Limit, and Actual output of a 80 M rotor turbine

* cutoff speed

Power Curve for Vestas V80 Wind Turbine from Vestas Brochure

Example calculation for power values in column 3 of the table:

ρ = density of the air
A = swept area of turbine’s rotor
v = velocity of the wind

Thus combining the equations for kinetic energy and wind speed, the power available in wind comes out to:

½ ρAv³

Air density (ρ) is about 1.2 kg/m³ at sea level and a temperature of 20 °C. This number varies depending on temperature and altitude. For example, in Colorado air density is about 1 kg/ m³ or 20% less than at sea level.

Using a Vestas V80 turbine with an 80 meter rotor as an example, the amount of wind energy available in a 20 mph (9.8 m/s) wind for this turbine with 5027 m² of swept area is:

½ × 1.2 kg/m³ × π × (40 m)² × (8.9 m/s)³  = 2.3 × 10⁶ kg·m²/s³  =  2.3 MW